Warum stellt man Pi eigentlich immer in unserem 10er-Zahlensystem dar? Ein Anthropologe erklärte einmal, das müsse wohl daran liegen, dass der Mensch zehn Finger habe - wieso sonst sollte er die Zehn für eine besondere Bündelgröße erachten? Hätte er zwölf Finger, dann würde er vielleicht mit dem (eventuell noch schöneren) Duodezimalsystem zur Basis 12 rechnen?
Das Binärsystem nimmt nun eine Sonderstellung unter den Zählsystemen ein. Überträgt man Pi ins Binärsystem, erhält man eine Zeichenfolge wie diese:
11,
00100100 00111111 01101010 10001000
10000101 10100011 00001000 11010011
00010011 00011001 10001010 00101110
00000011 01110000 01110011 01000100
10100100 00001001 00111000 00100010
00101001 10011111 00110001 11010000
...
Diese Folge provoziert zuallererst die Zählung nach der Verteilung von Nullen und Einsen. Bei der Analyse der ersten 32.000 Binärstellen kam ein sehr ausgewogenes Verhältnis heraus.
Spannender wurde es, als ich nach einer einfachen, aber attraktiven und aussagekräftigen Analysemethode vorging, das ich bei Roulette-Permanenzen zur Analyse von Rot-und-Schwarz-Folgen schon ausprobiert hatte.
Man beginnt wie folgt: Zählt, wie oft die erste Zahl, hier eine Eins, hintereinander kommt. In diesem Fall ist es die 11 vor dem Komma, man hat 2 Einserstellen - dann zählt man die Nullerstellen, die folgen. Es sind ebenfalls 2. So erhält man in der Matrix (1/0) eine Eintragung bei 2 links-vertigal und 2 rechts-horizontal oder [2/2].
Die zweite Matrix füllt sich mit den umgekehrten Werten, nämlich wenn die 0 auf die 1 wechselt (0/1). In unserem Fall folgt auf die zwei Nullen eine Eins, was eine Eintragung von [2/1] ergibt.
Ich habe die ersten 2.044 Binärstellen in die Matrix übertragen und folgende zwei Matrizen erhalten:
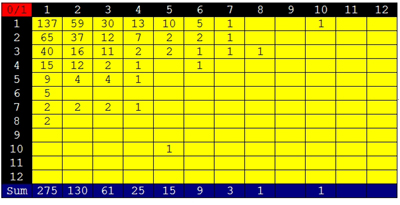
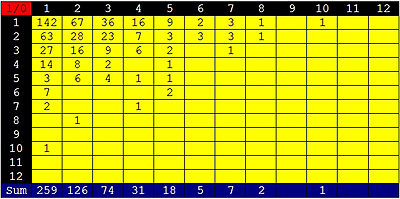
Es sind noch nicht ausreichend Werte zusammengekommen, man kann folglich beiden Matrizen nur Tendenzen entnehmen, die man bei eingehenderen Analysen nachprüfen kann auf ihren etwaigen Grad der Abweichung von einer gemittelten Norm. Auffällig sind aber einige Komplementaritäten zwischen den Matrizen, so dass viele Werte gemeinsam, also wenn man beide Matrizen addiert, insgesamt eine stimmigere Verteilung ergeben.
Anmerkung: Der Wert für [1/1] müsste bei einer idealen Zufallsverteilung doppelt so hoch sein wie der für [1/2] und [2/1], und viermal so hoch wie der für [2/2], [3/1] und [1/3] etc..
Eingehende Analysen der Pi-Binärverteilung werden folgen. Eventuell lässt sich sogar mit der Binärverteilung die Zufallsanalyse von irrationalen Zahlen am einfachsten und konkretesten ermitteln - die weiteren Untersuchungen werden das zeigen ...




