Wie beschreibt man am Besten den Unterschied der 0. Iteration zur 1. Iteration? Denken Sie sich einmal eine Zahlenfolge mit drei möglichen Werten: 1,2,3. Sie haben nun folgende Zahlen vorliegen:
23111223322111223
Die erste Iteration macht nichts anderes als zählen. Sie stellt fest, dass Sie hier 6x die Zahl 1 vorliegen haben, 7x die Zahl 2 und 4x die Zahl 3. Statistisch gesehen müssten Sie jede Zahl 17/3x vorliegen haben, also 5,666 mal. Sie könnten nun mit Hilfe der 0. Iteration die Standardabweichung errechnen und auch den Wert von  (0).
(0).
(Machen Sie das ruhig, wenn Sie meine Formel anwenden lernen möchten!)
Die erste Iteration nun bestimmt die Reihenfolge, in der die Zahlen "gezogen" werden. Da die erste Zahl eine 2 ist, steht die Zahl 2 folglich oben. Die zweite Zahl ist eine 3, also haben Sie jetzt eine Reihenfolge von 32 - woraus sich auch die dritte Stelle automatisch ergibt, also eine "321" (nachfolgend auch Pattern genannt). Sie haben nun gemäß der Glaukos-Iteration eine vollständige Reihenfolge bzw. Abfolge vorliegen und können jetzt eine weitere Zahlenkolonne anfügen, oder mit anderen Worten: die Zahlenfolge von der 0. Iteration in die 1. Iteration übersetzen.
Wenn Sie nun wie in diesem Beispiel ein "321"-Pattern ermittelt haben und in der Zahlenkolonne an dritter Stelle die Zahl "1" vorfinden, dann bedeutet das, dass Sie nun im "321"-Pattern nach der Stelle suchen, an der die 1 steht - an dritter Stelle. Womit Sie eine "3" ermittelt haben, die Sie nun als solche festhalten; Sie haben die erste Zahlenfolge also transkribiert. Um den Vorgang nun abzuschließen, müssen Sie das "321"-Pattern aktualisieren, jetzt rückt die 1 an die erste Stelle und Sie haben nun ein "132"-Pattern. Mit der Sie die nächste Stelle der Ausgangszahlenfolge übersetzen. Was dann wie folgt aussähe bei unserer Zahlenfolge:
0.Iteration: 23111223322111223
1.Iteration: xx311313121311213
Sie sehen, die Zahlenfolge wird etwas kürzer. Sie haben nun lediglich 15 Werte als Ergebnis. Bestimmen Sie nun von diesem Ergebnis die Häufigkeiten, haben Sie die Häufigkeiten der 1. Iteration vorliegen. In diesem Fall: 8x die Zahl 1, 2x die Zahl 2, 5x die Zahl 3.
Erneut können Sie nun die Varianz und Standardabweichung berechnen und auch den Wert von  (1). Wobei eine Kleinigkeit noch bemerkt sei: Sie sollten bei den Iterationen, wenn Sie sie vergleichen wollen, darauf achten, dass die gleiche Häufigkeit - also die gleiche Länge der Zahlenkolonne - verwendet wird. Also könnten Sie in diesem Fall die ersten beiden Zahlen der 0.Iteration löschen.
(1). Wobei eine Kleinigkeit noch bemerkt sei: Sie sollten bei den Iterationen, wenn Sie sie vergleichen wollen, darauf achten, dass die gleiche Häufigkeit - also die gleiche Länge der Zahlenkolonne - verwendet wird. Also könnten Sie in diesem Fall die ersten beiden Zahlen der 0.Iteration löschen.
Dieses Verfahren lässt sich nun theoretisch bis in die "Unendlichkeit" fortsetzen.
Die Ermittlung der Iterationen ist jedoch nur dann wirklich sinnvoll, wenn auf diesem Weg tatsächlich ein Plus an Information erzeugt werden kann. Aber ist das tatsächlich der Fall? Ich habe die 1. Iteration an den 20 Irrationalzahlen vorgenommen (was ohne Verwendung eines Computerprogramms 12 Stunden Arbeit verursacht und hin und wieder vermutlich einen kleinen Fehler einschleichen lässt):
Hier können Sie wieder das gesamte Tableau der einzelnen Werte von  (1) in einem Popup einsehen.
(1) in einem Popup einsehen.
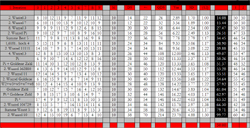
Beginnen wir mit der Häufigkeitsverteilung:
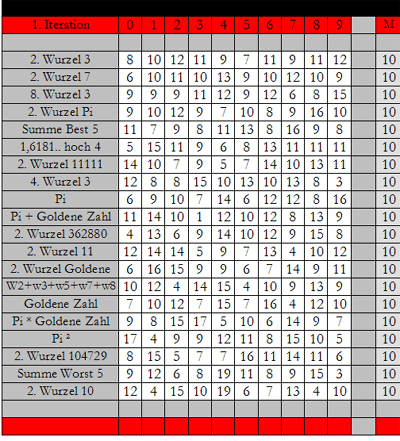
Zum Vergleich die 1. Iteration:
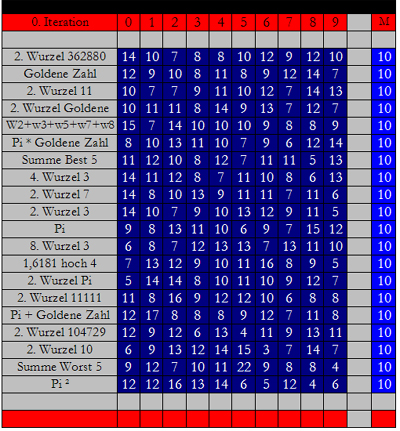
Was sehen Sie? Vermutlich noch nicht viel, wenn Sie sich nur die Zahlen ansehen ...
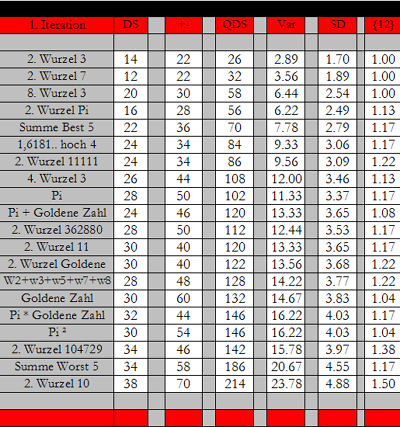
Hier die einzelnen Parameter von  (1):
(1):
Und hier die Werte von  (1), die die Reihenfolge des Rankings festlegen:
(1), die die Reihenfolge des Rankings festlegen:
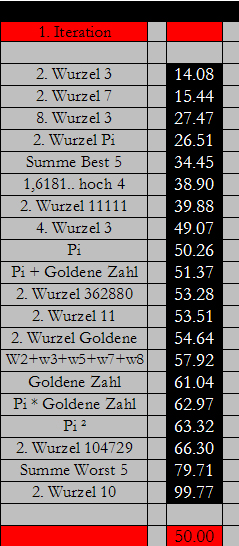
Und hier noch einmal das Ergebnis der 0. Iteration:
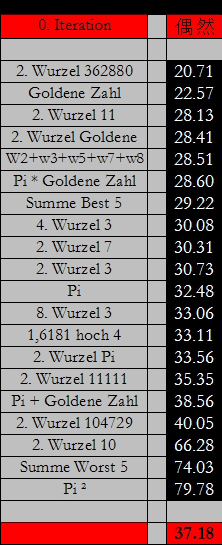
Hier springen einige Ergebnisse schnell ins Auge:
Das Spektrum hat sich geweitet, die Werte von  (1) bewegen sich zwischen 14,08 und 99,77, während die Werte von
(1) bewegen sich zwischen 14,08 und 99,77, während die Werte von  (0) enger gefasst sind zwischen 20,71 und 79,78.
(0) enger gefasst sind zwischen 20,71 und 79,78.
Zweitens: Der Durchschnittswert von  , wenn man alle 20 Werte berücksichtigt, liegt mit 50.00 gegenüber 37.18 von der 1. Iteration zur 0. Iteration deutlich in Richtung Abweichung vom Erwartungswert.
, wenn man alle 20 Werte berücksichtigt, liegt mit 50.00 gegenüber 37.18 von der 1. Iteration zur 0. Iteration deutlich in Richtung Abweichung vom Erwartungswert.
1. Deutung: Die 1. Iteration sorgt für eine weitere Sortierung und in der Sortierung für eine Präzisierung, denn auf diese Weise weitet sie das Spektrum, holt die Unterschiede zwischen den einzelnen Zahlenkolonnen heraus.
Weitere Auffälligkeit: Die 0. Iteration hat sehr viele Werte von  (0) innerhalb von 28 und 34. Bei der 1. Iteration ist die Streuung regelmäßiger, nur eine leichte Ballung ist zwischen den Werten 49 und 63 zu erkennen.
(0) innerhalb von 28 und 34. Bei der 1. Iteration ist die Streuung regelmäßiger, nur eine leichte Ballung ist zwischen den Werten 49 und 63 zu erkennen.
Interessant ist auch dies: Die Irrationalzahlen mit sehr geringem  (0) wie die Goldene Zahl oder die zweiten Wurzeln aus 11 und 362880 rangieren in der 1. Iteration sehr weit hinten.
(0) wie die Goldene Zahl oder die zweiten Wurzeln aus 11 und 362880 rangieren in der 1. Iteration sehr weit hinten.
Anders an der unteren Skala: 4 von 5 der schlechtesten Werte von  sind in beiden Iterationen am Ende der Skala zu finden.
sind in beiden Iterationen am Ende der Skala zu finden.
Hier die beiden Iterationen im direkten Vergleich ihrer Durchschnittswerte:

Es wird klar ersichtlich, dass bei allen Kriterien die 1. Iteration eine größere Streuung aufweist - lediglich bei {12} erhält man einen gleichen Wert.
Eine kurze Erläuterung: DS zeigt, dass die Häufigkeiten vom Erwartungswert "10" bei der 1. Iteration stärker abweichen. +- zeigt, dass innerhalb der Zahlenfolge bei der 1. Iteration eine größere Schwankung zu verzeichnen ist. QDS entspricht der VAR und der SD - und zeigt hier eine größere Abweichung der 1. Iteration vom idealen Mittelwert. Lediglich {12} zeigt an, dass innerhalb der Zahlenfolge die Zahlenwerte 0-4 genauso gleichmäßig verteilt sind wie die Zahlenwerte 5-9 (bzw. die Zahlen"positionen" im Falle der 1. Iteration, wenn man genau sein möchte ...).
Prognose: Man könnte an dieser Stelle eine Prognose wagen, wie sich die Werte für die folgenden Iterationen gestalten werden; könnte vermuten, dass sie weiter differieren werden. Dass sich das Spektrum der  (x) immer weiter auseinanderbewegen wird und ihr Durchschnittswert weiter anwächst.
(x) immer weiter auseinanderbewegen wird und ihr Durchschnittswert weiter anwächst.
Weitere Untersuchungen mit der 0. und 1. Iteration habe ich anhand der Kreiszahl Pi durchgeführt. Sie finden die Analyse auf dieser Seite.









